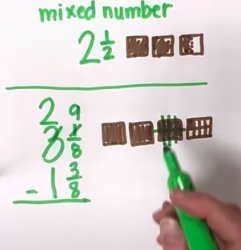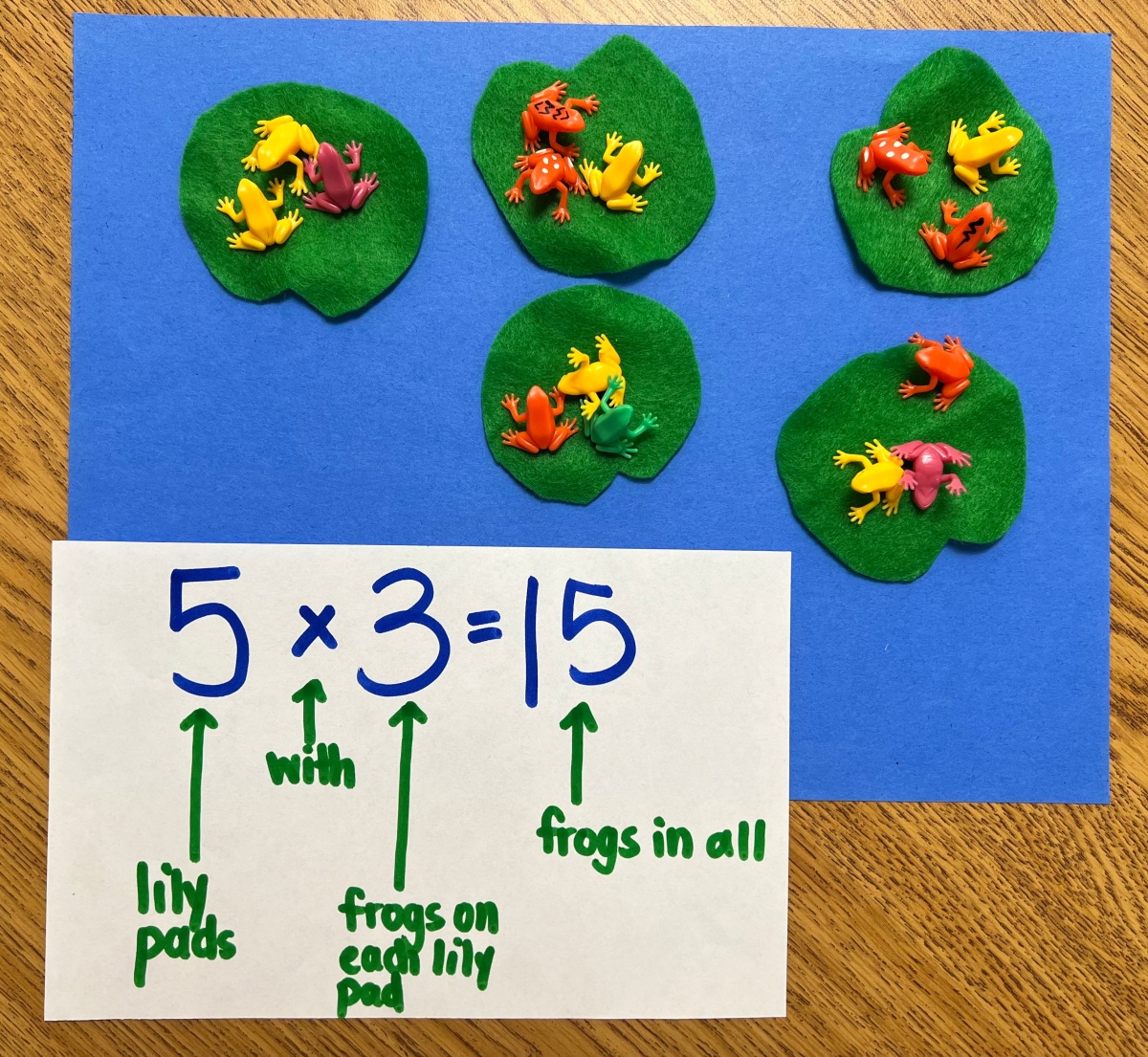Tag / elementary math

by Beyond Traditional Math

5 Tips for Making Anchor Charts Like a Pro

It breaks my heart when I hear elementary teachers shamefully tell me that they were “never good at math”, hated math or just don’t feel confident. The truth is, if this is you, it is a GIFT. If you never felt confident in math, then you know exactly how your students feel. Not only that, it will make you an anchor chart machine.

Anchor charts are the missing link between our instruction and students practicing mathematics. We as teachers may have taught a concept 5 years in a row or more, but for students it could be their first time hearing it. They also may have holes missing in previous years instruction for a variety of reasons. Giving students what they need right up on their wall is the first step in helping them make connections, remember complicated processes or learn brand new vocabulary. You have English Language Learning students? Special Education students? It doesn’t matter who is in your classroom, anchor charts are good for ALL of your students.

Take this anchor chart for a grade 2 unit on number lines for example:

There are things on that anchor chart that every single adult takes for granted. We know what a tick mark is, we know what a point is, and we know what to do when numbers are missing. These are things that the majority of our students have never experienced. This anchor chart is especially important because number lines come up in so many concepts for many years to come.

Anchor charts are best made when you think about the following 5 things:

  1. How can we make it together? This is critical. When learning is synthesized at the end of a lesson, that’s the perfect time to add to your anchor chart, and as much as possible written in student friendly language.
  2. What new math specific vocabulary needs to be explained on the chart? Act like a new learner, like you’ve never heard some of these words before. Which belong on the anchor chart? How can words be written with precision, but still student friendly? Anchor charts explain that we can use math words like point instead of dot or tick mark instead of line.
  3. What misconceptions do students have? What is important to remember, and what errors are you are seeing your students make in the lessons?
  4. What is the least amount of words I can put on it? Visuals are KEY. The more visuals you have the better! They are both engaging and beautiful. Some of the anchor charts I’ve seen are absolute works of art.
  5. How new is this material to my students? If they haven’t had prior exposure to the concept, it MOST definitely belongs on your wall.

This is not an exhaustive list, but a place to start. The more you work on anchor charts the better you will get at them. As you walk around helping, you’ll notice a lot of the same questions keep on getting asked. This is an instant signal that you need to get that up on the wall to help mass amounts of students.

I wish this is something that I would have known when I was a first year teacher, when I thought I was bad at teaching math. It would have been an incredible thing to really think through all those things that I struggled with as a student, learn along side them and provide the proper supports.

Advertisement
by Beyond Traditional Math

3 Tips to Help Students Tell the Difference Between Area and Perimeter

For as long as I can remember students have mixed up the difference between area and perimeter on standardized tests. Around this time of year as state testing approaches, we all get this nutty feeling that we need to start hammering test prep activities and get out flashcards with vocabulary. Here are three easy ways to ease your test prep anxiety and get students engaged with these two concepts.

First: make it part of your every day practice. For example, when it’s time for a class meeting and you’d like them to sit in a circle, make it a rectangle instead and ask them to sit on the perimeter of the mat/rug. “Please go to your perimeter spot.” When it’s time for a mini lesson, have them sit in the area part of the mat. “Please have a seat in your area spot.” Take a picture of them in both of those spots and label it on an anchor chart during your beginning of the year routines.

Second: use visuals like anchor charts during your lesson, and then keep up after your lesson on your walls. Check out this real world connection from Fifth in the Middle:

Once they understand the real world application, you can then talk through a more abstract model for your anchor chart (which is much more like what they will see on a standardized test):

Third: Try some deep thinking activities that will get them applying the concepts. Press play on the video below to see it in action. You can try one for free by clicking the link for PILES and downloading the preview. The activity is SO engaging and sometimes more effective because it’s not a worksheet. I love it because we have so many representations on standardized tests, and this takes some of the pressure off of test prep.

by Beyond Traditional Math

Teen Numbers are Early Place Value

Teen numbers in English are STRANGE. I mean, look at these weirdos in the first half of the numbers:

11 – eleven (not one teen)

12 – twelve (not two teen)

13 – thirteen (not three teen)

14 – fourteen

15– fifteen (not five teen)

16 – sixteen

17 – seventeen

18 – eighteen

19 – nineteen

When we start teaching these numbers to our youngest learners, we often take for granted the strangeness of the names of these numbers.We are used to the names and counting with them…we don’t even question or notice how strange they are. The first half of them don’t even follow a logical pattern! In addition, I often hear videos being played where the singer is saying “Teen numbers start with a 1!” Actually, teen numbers are written with a 1 first yes, but that one in the teen number does NOT have a value of “one”.

Teen numbers are the basis of place value. I still work with third graders who will see 10+6 and start counting on their fingers to figure it out! How they don’t know that shortcut always shocks me. I think somewhere we failed them in understanding the value of the 1 in the teen number.

Beginning to learn about place value for our early learners needs to include some key things. We have to spend a lot of time letting them play with the numbers, get comfortable with different representations of those numbers, including finding the ten that is hiding in the number. In many state standards teen numbers are expected to be thought of/written as a group of 10 and some more ones. YES, this is key! In the photo below you’ll see some of these various representations with fingers and numbers. In future posts, I’ll show some other representations and tools that work AWESOME.

In addition concrete tools should also be incorporated as much as possible! Here we are using units of one and ten to make it match the fingers. Very powerful for them to connect a tool from their body (fingers) to a more abstract tool (base ten blocks).

Never skimp on those teen numbers kindergarten teachers! Future grade levels depend on you to explore these concepts deeply with your students.

by Beyond Traditional Math

How to Subtract and Regroup Mixed Numbers with Visual Models

Flashback to 4th grade when my math teacher asked me to subtract mixed numbers, my palms were sweaty, and I felt like I was looking at the demonstration cross eyed WITH brain fog. If you are a loyal follower of my blog, you might know about my past traumatic experience with fractions. It was not pretty, and the last thing I want is for any student of mine to feel this way.

I created the video below to try to show regrouping with visual models. I can’t stress enough how visual models have changed and revolutionized my teaching. It almost never fails that when students struggle, I’ve forgotten to include a visual to help them “see” the math. I am not alone, check out Dr. Jo Boaler, Berkeley Everett and many others who truly understand how we can deeply teach mathematics through visual representations.

The video below will speak for itself, but if you don’t have time to watch it (it’s less than five minutes), the idea is that you can regroup whole numbers into fractions just like students do with base ten models. It’s SO MUCH FUN when students get to learn this way with you. Please check it out and let me know what you think!

by Beyond Traditional Math

Start Geometry Vocabulary Early!

I love to be sneaky with using vocabulary in the classroom. One of the ways that I like to embed it is through game playing. For example, instead of using two color counters, we pull out the pattern blocks. Instead of saying “I want blue!”, I tell the students that I would like them to sound more like a fancy mathematician. Instead you must say, “I would like to play with the trapezoid, please.” It causes a laugh with the kids, but even better it starts to get them to use those words more regularly and with purpose. Plus they love to say the word trapezoid! There is a nice benefit to getting these words in their mind early, they’ll start to connect that vocabulary to real world examples of lines, points, segments and other geometry terms.

There is a natural reason to determine the difference between the two tools in the photo below, and to examine how the rhombus and trapezoid are different so that they know which one to pick. This can start as early as the primary levels! Most pattern block sets come with hexagons, triangles, rhombuses, parallelograms, and trapezoids.

by Beyond Traditional Math

I’m Taking a Big Risk!

I used to hate teaching math when I began my education career. It was scary! I didn’t know what I was doing and had ZERO confidence. 18 years later, you’ll find me traveling across the country teaching other teachers the best ways to teach math. My number one goal in starting this blog is to help YOU love to teach math. However, blogging isn’t the main form of learning these days. I find myself going to social media to learn so many things. So…I am (very nervously) trying a new idea where I do things way beyond my skill and comfort level:

  1. I have started an instagram account (a professional one), you’ll find it by clicking here: @beyondtmath
  2. My goal is to release as many teaching tips as I can using reels or video posts.
  3. I want every video to be under 60 seconds, and something you can try immediately.
  4. I plan to try to do these weekly.

It feels worrisome to put myself out there, but I’m going to be posting all those tips that I tell teachers and I hear back: “I wish someone had told me this!” or “I love that idea!” or “I am SO trying that!” or “That finally makes sense to me!”

My first post is about how to develop number sense with cubes. I hope you’ll venture over and find me! (Please, please, please!)

How to teach number sense.
by Beyond Traditional Math

The Absolute BEST Way to Practice Multiplication Facts

Flashcards are the worst for practicing fact fluency. I’m just going to say it. They are JUST the worst. Actually maybe timed tests are the worst, but we will tackle that another day. Talk about taking all the joy and fun out of mathematics. They only work for students who can memorize, and while you might be thinking “Hey! They worked great for me!” You were probably one of the lucky ones. Even if they DO work for SOME kids, is that the best way to practice math facts?

My favorite, favorite, favorite thing is to have students play with multiplication first. Multiplication fact practice doesn’t have to be devoid of all fun. You start out by purchasing really great things that are high interest for children, and then find a way to help them put them into groups. We use fake eggs and egg cartons, pop its to show rows with pressed in dots, penguins on icebergs and the fan favorite among every student I’ve ever done this with…is the mini shopping carts with groceries.

Practice multiplication facts with fake eggs
Practice multiplication with pop its
practice multiplication facts with penguins and icebergs
practice multiplication facts with mini grocery carts

As long as the items can be put into groups, they can represent multiplication. Now in this case you can actually pair flashcards with these items. Pick a flashcard, then build it. This will help your students make some meaning out of the number sentences. The more students build their multiplication facts, the faster they learn the meaning of multiplication conceptually. The faster they learn the conceptual part, the easier time they have visualizing multiplication. The easier time they can visualize multiplication facts, the faster they can learn strategies for skip counting or doubling groups. It snowballs quite quickly! I’m a huge proponent of games and activities like this vs. time tests and flashcards. This does a lot of great things for students:

  1. It reduces anxiety big time and adds in play, which research shows allow you to be a better problem solver.
  2. Students start to look for shortcuts (our brains are wired this way), and they will begin to skip count rather than count by ones to find the total.
  3. It normalizes the use of tools for ALL students.
  4. Eventually these items won’t be needed, as they will eventually become tired of building the items and will come up with other ways to solve multiplication facts.

This is an awesome thing to work on at your teacher table, or to have as an ongoing station for students to play around with during independent work time in your math workshop.

by Beyond Traditional Math

Real Life Examples of Multiplication

The switch from working with addition/subtraction to multiplication/division for students can be pretty jarring. With multiplication, everything they have previously known about abstract symbols suddenly changes from straight up just adding what you see to adding groups or rows. While many students can successfully use multiplication, I will often see the writing of number sentences to be full of small errors. I’ve found the best way to clear up those errors is to use really engaging REAL WORLD multiplication examples.

For instance, in the image below, you can see five lily pads with 3 frogs on each lily pad. The number sentence that matches this story could be 5 x 3, because there are 5 groups of 3 frogs. I love to help them make sense of the symbols and numbers by simply labeling that number sentence (see pic below), and then having them work through several examples.

You can have them practice this skill in a few ways:

  1. Write the number sentence and have them build it. Do it over and over, until they get used to the first number being how many group they need.
  2. Build it for them and have them write a matching number sentence.
  3. Give them a number sentence, build it incorrectly and then have them find your error. (THEY LOVE THIS!)

The more practice they get with these concrete items, the faster it will settle in, and the more confident your student will feel!

by Beyond Traditional Math

How to Stop Meaningless Problem Solving

Today while working with some third graders in my intervention group, I had that moment that I know you all have as a teacher. When you pose a story to be solved (I’m tired of calling them problems…is it ok to call them stories to be solved?), and the students just start panic crunching numbers. Like throwing numbers around and adding up every number they hear in the story.

Today it was simple story, one that I know these three could probably picture in their minds, or at the very least draw:

“There are two trees, each one has 15 cherries. How many cherries are there altogether?”

I’ve been reading about the benefits of using vertical white board surfaces, to get students to do more thinking. One student wrote 2 + 15 = 17 with her partner. She was CONVINCED (and there was nothing I could say to change her mind), that because there were two trees and 15 cherries, those two numbers must be added together. The other student knew to add 15 and 15, but used an inefficient strategy of drawing each individual cherry on the two trees. I will address the inefficient strategy issue in another post, but today I really want to address the idea of students just crunching numbers without thinking.

I think for too long, students who struggle with math have been led down this road of not have the proper exposure to tools, drawings and then the abstract notation of mathematics. I see tools disappearing as early as first grade in classrooms, which we all KNOW are critical in child development. Not only are tools disappearing, but I see math programs that encourage abstract notation before connecting tools and drawings to that notation.

Take for example, 3 x 14 or 14 x 3. This student was able to build it with tiles (showing an understanding of area), then was able to take a shortcut and show an area model (without the tiles inside), and eventually use partial product notation to solve.

Somewhere along the line, students who struggle to problem solve missed these connections. They look at you with panic in their eyes as they try to figure out what you are asking and what they have to do. Then in pure desperation instead of solving, they just start mindlessly crunching numbers, not making any connections whatsoever.

Here are some ways that I intervene:

  1. Make tools available, have them act it out first, then draw what they made. Don’t worry at this point if the notation is correct, can they make sense of the problem with tools? At first it might be helpful to provide the tool, then the next time have a few different ones to choose from. Start watching if they are choosing an appropriate tool.
  2. Write a hint in a different color. Explain that the hint will lead them in a different direction, and that they need to “unthink” some part of what they did. In the case of the cherry trees, I drew an additional tree next to the one they had already drawn and wrote 15 under it. That little hint made all the difference.
  3. Look for places they are actually making connections and compliment them on that. The student who wrote 2+15 was actually thinking about multiplication! I told her that, but then asked the two of them to back up and think about what that would mean if they multiplied those two numbers. Find SOMETHING that you like about what they did. Those compliments stick, and they remember it again next time and will use it.
  4. Don’t give up on them, and have high expectations. I hear this said over and over again, “My ‘low’ students have a really hard time problem solving.” When you call them low, you will expect nothing but low performance.
  5. Try not to give the answer at the end. Explain that problem solving is about thinking, not the answer. This will enrage them at first, but eventually they will start thinking instead of spitting out an answer. They will also see that they need to persevere while solving instead of waiting for the teacher to give the strategy and answer in the end.
  6. Have them compare two strategies next to each other. Have the students look for similarities and difference.
  7. Choose random partners whenever possible. This allows students to learn different strategies from others, and it keeps your groups fresh.

Students who struggle in mathematics can be excellent problem solvers. It’s so critical that we believe this, and that we continue to challenge them at high levels with the right supports.

by Beyond Traditional Math

Test Prep without Pain

Math test prep for spring standardized testing is always a bit daunting. Teachers face the same dilemma every year:

  1. Trust that we’ve taught everything we need to teach and go in with the confidence that students can apply it….
  2. Panic about things such as spiral review, cram in one last topic/unit, review vocabulary words and teach best test taking tips…

Both of those options are perfectly okay, but both make teachers and students feel a bit uncomfortable.  Without teaching any test prep, we worry that students won’t be able to “figure out” questions. Students feel nervous not knowing what to expect and want to feel confident going in. But too much test prep stresses out the teacher and the students, putting tons of pressure on them as they go into a testing situation.

I propose some test prep (for math anyway) without the pain of these feelings.  I came up with Reasoning Puzzles when we first began teaching with the Common Core State Standards.  As I looked at our state test, last year I realized the rigor has most definitely increased, especially the ability for our students to take apart questions and look for multiple solutions and answers.

Instead of flashing up multiple choice questions, students participate in small group discussion about “puzzles”and statements about those puzzles. Allowing them to talk over these puzzles, and make their mathematical thinking visible to each other, they become much more confident.  Testing truly is just trying to make sense of a problem, and looking for small nuances in how the question is asked, combined with calculations of some sort. This sort of test prep is fun, builds confidence in your students, and if done all year can create very powerful mathematicians.

I used them with my own third graders for years, and now with my intervention students.  I received a tweet from a woman named Lisa who took it even a step further and had her students write their own statements. What a great way to extend the learning!

test-prep-math-standardized-testing

test-prep-math-standardized-testing2

Reasoning Puzzles give students a chance to think critically and to use the standards for mathematical practice effectively.  Feel free to check out the free sample to try them yourself if you’d like.

math-test-prep-standardized-testing